This is the third post in a three-post series. In the first post we developed a stack-safe, ergonomic, and concise method for working with recursive data structures (using a simple expression language as an example). In the second post we made it fully generic, providing a set of generic tools for expanding and collapsing any recursive data structure in Rust.
In this post we will see how to combine these two things - expanding a structure and collapsing it at the same time, performing both operations in a single pass. In the process, we will gain the ability to write arbitrary recursive functions over traditional boxed-pointer recursive structures (instead of the novel RecursiveTree type introduced in my previous post) while retaining stack safety.
This post covers functionality already implemented in my recursion crate. For that reason, it will focus on diagrams over code, but the relevant code is provided if you’re interested or curious.
Our Expression Language
Earlier in this series we defined a simple expression language for math, using this enum to represent a single layer of an expression tree:
pub enum ExprLayer<A> {
Add { a: A, b: A },
Sub { a: A, b: A },
Mul { a: A, b: A },
LiteralInt { literal: i64 },
}
struct ExprBoxed(Box<ExprLayer<ExprBoxed>>);
So that we can easily write expressions out by hand (for test cases and examples), let’s define some helper functions (specifics omitted).
// some simple utility functions for creating boxed expressions
impl ExprBoxed {
fn add(a: Self, b: Self) -> Self { ... }
fn sub(a: Self, b: Self) -> Self { ... }
fn mul(a: Self, b: Self) -> Self { ... }
fn literal_int(x: i64) -> Self { ... }
}
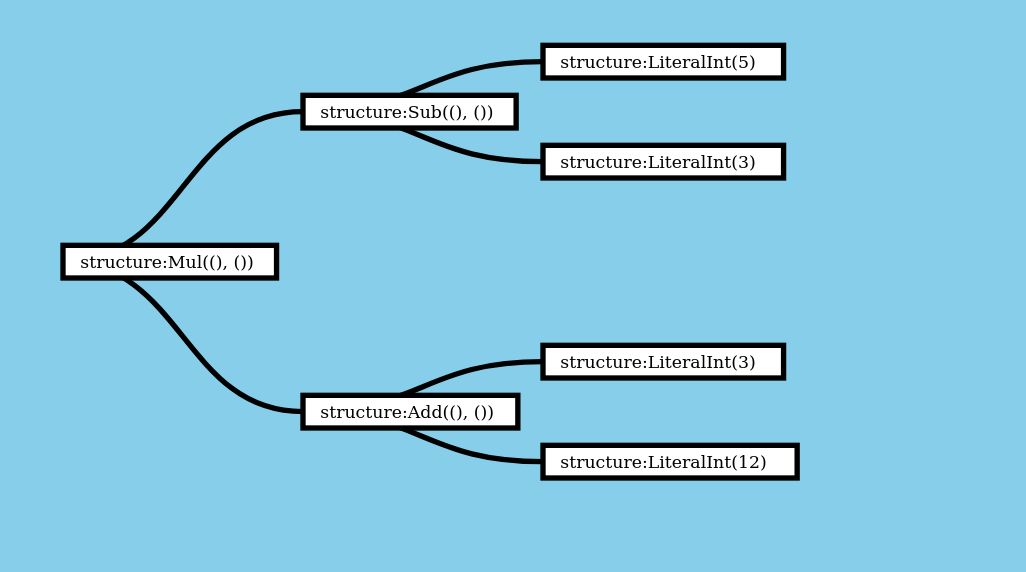
In this post we’ll be working with the expression (5 - 3) * (3 + 12). Here’s what that looks like as code:
use ExprBoxed::*;
let expr = mul(
sub(literal_int(5), literal_int(3)),
add(literal_int(3), literal_int(12)),
);
Expand and Collapse
Previously, we defined two core traits representing the ability to expand a recursive structure out from some seed, and to collapse a recursive structure down into a single value:
/// Support for expanding a data structure from a seed value, one layer at a time
pub trait Expand<A, Wrapped> {
fn expand_layers<F: Fn(A) -> Wrapped>(a: A, expand_layer: F) -> Self;
}
/// Support for collapsing a data structure into a single value, one layer at a time
pub trait Collapse<A, Wrapped> {
fn collapse_layers<F: FnMut(Wrapped) -> A>(self, collapse_layer: F) -> A;
}
We’ll be introducing a new recursion backend that implements these traits. This is already implemented in the recursion crate, so this post is concerned mostly with communicating the underlying concepts - not the implementation details.
Recursive Data Structure
Instead of using a vector of elements linked by vector indices, we’ll construct a vector where linkages are defined only by the relative position of elements. This lets us replace the usize vector indices used in the previous posts with zero-size markers (StackMarker, equivalent to () but given its own name for convenience). This results in an extremely compact representation of recursive structures.
Here’s what the data structure looks like. It’s provided by the recursion crate, so you won’t need to define it yourself.
pub struct StackMarker;
/// Recursive tree made up of layers of some type 'Layer<_>', eg `ExprLayer<_>`
pub struct RecursiveTree<Wrapped> {
/// nonempty, in topological-sorted order
elems: Vec<Wrapped>, // Layer<Index> (eg `ExprLayer<()>`)
}
Here’s a visualization of what this data structure looks like for the expression (5 - 3) * (3 + 12).
Expand
Let’s see what expanding a boxed expression tree for (5 - 3) * (3 + 12) into a RecursiveTree looks like. We’ll look at the implementation soon, but this visualization shows what the computation looks like.
You can see the implementation of expand_layers for this structure below, if you’re curious, but the important thing is that we have an implementation of Expand provided by the recursion crate, not how its implemented. The whole point of having a crate is not having to examine every implementation detail!
impl<A, Underlying, O: MapLayer<StackMarker, Unwrapped = A, To = U>> Expand<A, O>
for RecursiveTree<U>
{
fn expand_layers<F: Fn(A) -> O>(a: A, generate_layer: F) -> Self {
let mut frontier = Vec::from([a]);
let mut elems = vec![];
// expand to build a vec of elems while preserving topo order
while let Some(seed) = frontier.pop() {
let layer = generate_layer(seed);
let mut topush = Vec::new();
let layer = layer.map_layer(|aa| {
topush.push(aa);
StackMarker
});
frontier.extend(topush.into_iter().rev());
elems.push(layer);
}
elems.reverse();
Self {
elems,
_underlying: std::marker::PhantomData,
}
}
}
Let’s see what expanding a boxed-pointer expression into a RecursiveTree looks like. Since it’s already made up of ExprLayer layers, we can just dereference the boxed value using the * operator.
let expr_tree = RecursiveTree::expand_layers(expr, |ExprBoxed(boxed)| *boxed)
Collapse
Here’s what collapsing the RecursiveTree that we just constructed for (5 - 3) * (3 + 12) looks like. As in the last section, this visualization shows what the computation looks like.
impl<A, O, U: MapLayer<A, To = O, Unwrapped = StackMarker>> Collapse<A, O>
for RecursiveTree<U>
{
fn collapse_layers<F: FnMut(O) -> A>(self, mut collapse_layer: F) -> A {
let mut result_stack = Vec::new();
for layer in self.elems.into_iter() {
let layer = layer.map_layer(|_| result_stack.pop().unwrap());
result_stack.push(collapse_layer(layer));
}
result_stack.pop().unwrap()
}
}
Here’s how we can use this to collapse expressions represented in the RecursiveTree format. Nothing complex, just some simple arithmatic:
let result = recursive_tree.collapse_layers(|expr| {
use ExprLayer::*;
match expr {
Add { a, b } => a + b,
Sub { a, b } => a - b,
Mul { a, b } => a * b,
LiteralInt { literal } => literal,
}
})
Expand and Collapse in a Single Pass
As a reminder, the RecursiveTree representing (5 - 3) * (3 + 12) looks like this:
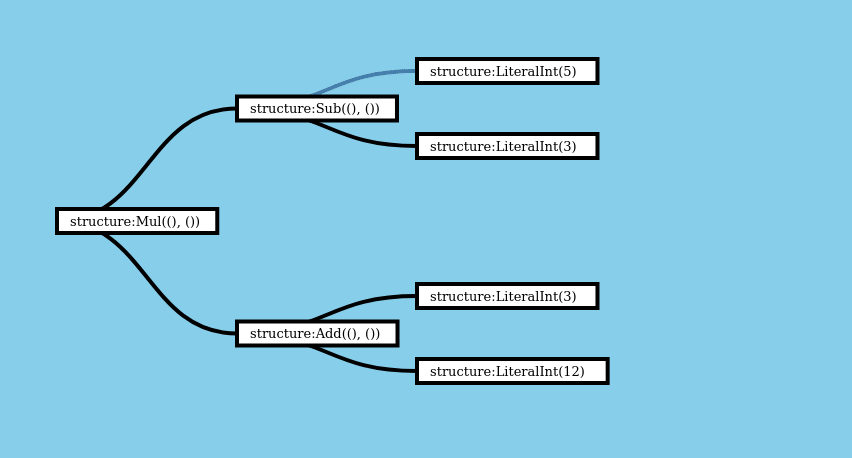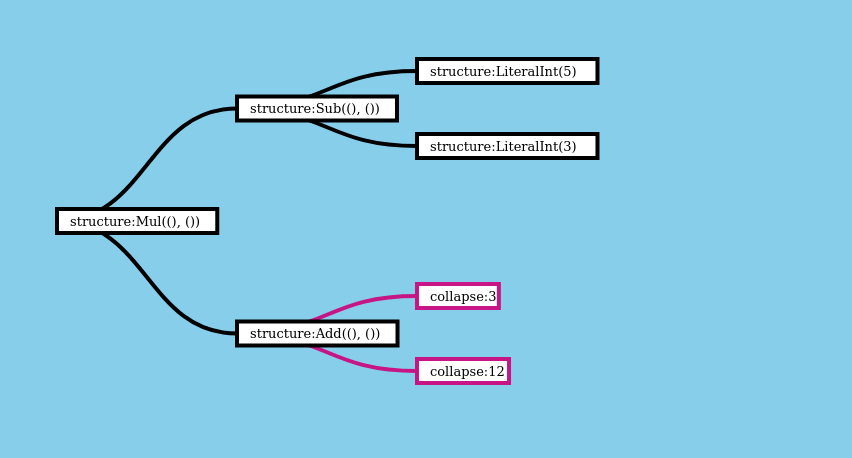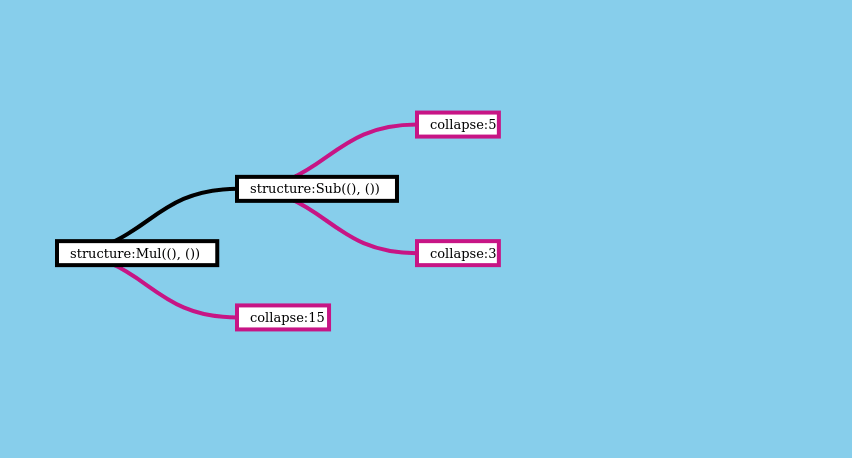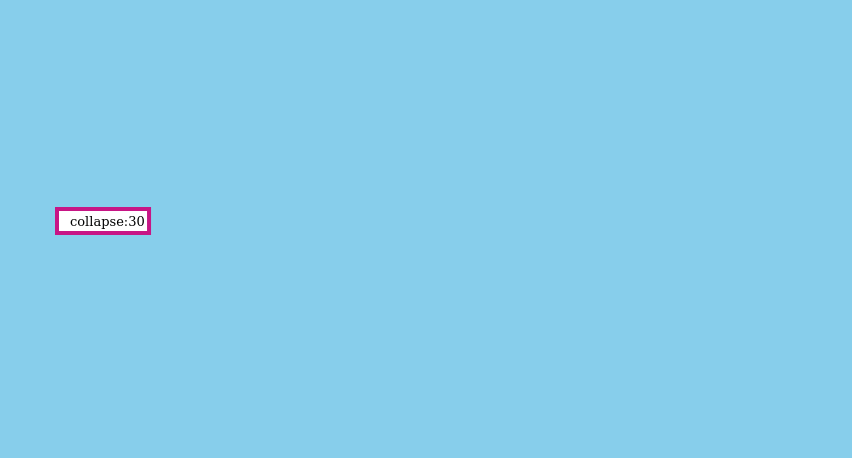
Here’s a visualization showing what the full evaluation looks like, if we run expand_layers immediately followed by collapse_layers:
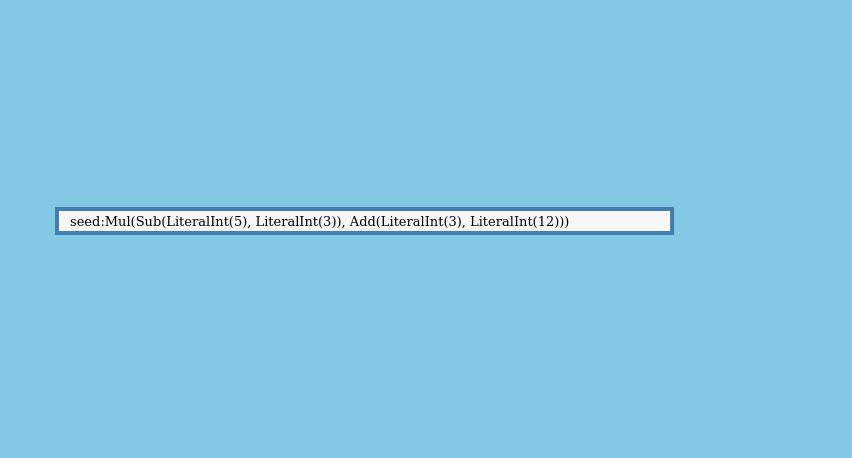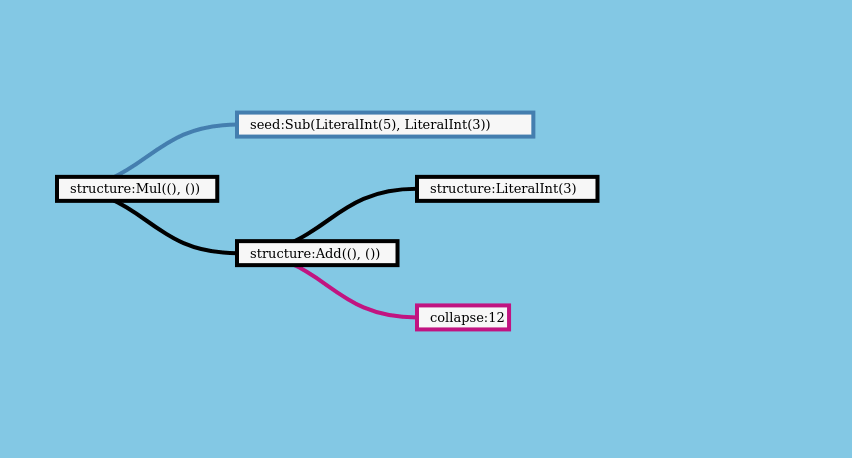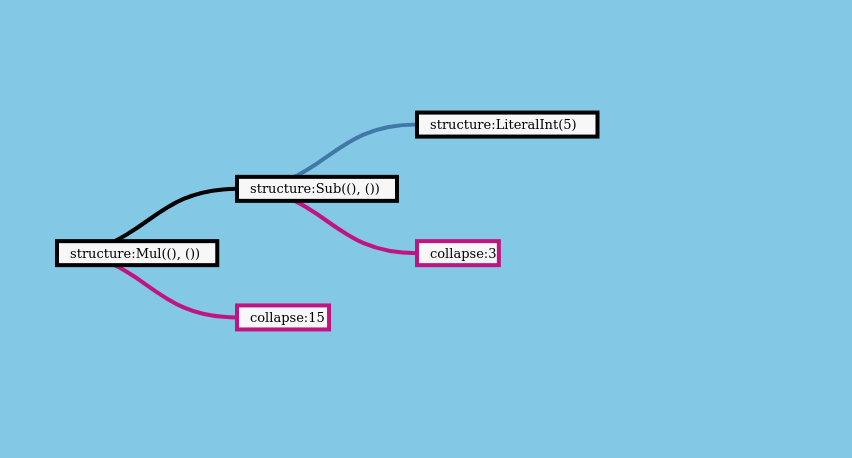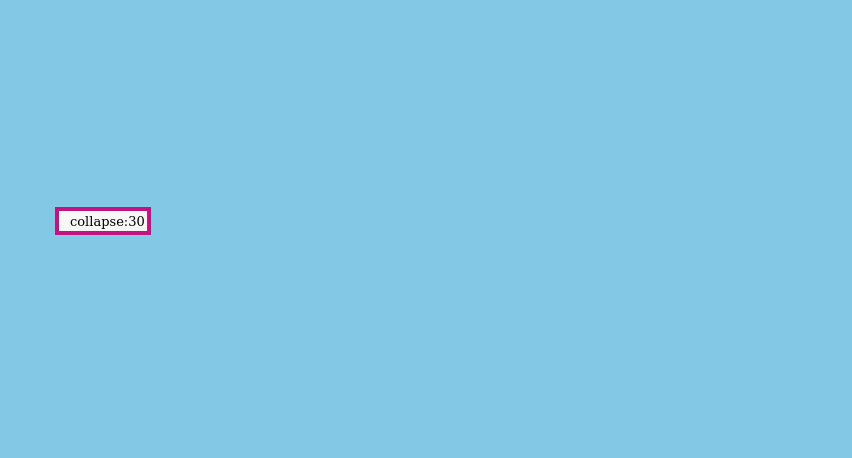
But what if could run both operations in a single pass? That would remove the need to hold the full tree in memory. It would also let us avoid introducing a new type of data structure - RecursiveTree - into our projects. It should be possible to evaluate the expression like this, one branch at a time, instead of constructing the full tree:
The function that does this is called expand_and_collapse, and it’s provided by the recursion crate. Docs are here.
/// For some Layer type, Expandable is Layer<Seed> and Collapsable is Layer<Out>
pub fn expand_and_collapse<Seed, Out, Expandable, Collapsable>(
seed: Seed,
mut expand_layer: impl FnMut(Seed) -> Expandable,
mut collapse_layer: impl FnMut(Collapsable) -> Out,
) -> Out
Expandable: MapLayer<(), Unwrapped = Seed>,
<Expandable as MapLayer<()>>::To: MapLayer<Out, Unwrapped = (), To = Collapsable>,
The full implementation is below, if you’re curious.
pub fn expand_and_collapse<Seed, Out, Expandable, Collapsable>(
seed: Seed,
mut expand_layer: impl FnMut(Seed) -> Expandable,
mut collapse_layer: impl FnMut(Collapsable) -> Out,
) -> Out
where
Expandable: MapLayer<(), Unwrapped = Seed>,
<Expandable as MapLayer<()>>::To: MapLayer<Out, Unwrapped = (), To = Collapsable>,
{
enum State<Seed, CollapsableInternal> {
Expand(Seed),
Collapse(CollapsableInternal),
}
let mut vals: Vec<Out> = vec![];
let mut stack = vec![State::Expand(seed)];
while let Some(item) = stack.pop() {
match item {
State::Expand(seed) => {
let node = expand_layer(seed);
let mut seeds = Vec::new();
let node = node.map_layer(|seed| {
seeds.push(seed)
});
stack.push(State::Collapse(node));
stack.extend(seeds.into_iter().map(State::Expand));
}
State::Collapse(node) => {
let node = node.map_layer(|_: ()| vals.pop().unwrap());
vals.push(collapse_layer(node))
}
};
}
vals.pop().unwrap()
}
Here’s how we can use this function to evaluate a traditional boxed-pointer recursive expression tree, without constructing an intermediate RecursiveTree - thus saving on both conceptual overhead and memory-usage overhead:
fn eval(expr: ExprBoxed) -> i63 {
expand_and_collapse(
expr, // seed value
|ExprBoxed(boxed)| *boxed, // expand layer function
|expr| {
// collapse layer function
use ExprLayer::*;
match expr {
Add { a, b } => a + b,
Sub { a, b } => a - b,
Mul { a, b } => a * b,
LiteralInt { literal } => literal,
}
},
)
}
This is fully generic, and can be used with any recursive structure, not just the simple expression language used in this post. In the next post, I’ll show how to use expand_and_collapse to build an expression language for matching filesystem entities, with features like short-circuiting to minimize syscalls, arena allocation (as a flex), and, of course, many more execution graphs.
Computer Science Implications
If you have a background in data structures and algorithms, and if you looked closely at the implementation details of the above functions, you might recognize them as implementing stack machines.
If you’re familiar with Haskell and Recursion schemes, you might recognize expand_and_collapse as a hylomorphism. If you don’t know what the hell a hylomorphism is and are interested in learning, there’s an excellent blog post here that goes into some detail on the concept.
There does appear to be a fundamental correspondence between stack machines and hylomorphisms. This is interesting, because these ideas arise in different corners of the computer science universe. That said, this isn’t that surprising, as both are descriptions of the same thing: recursion.
Thank you
Thank you to Fiona, Rain, Eliza, among others, for reviewing drafts of this post.